Correlation IS Causation!

Well, it's evidence of causation

Everybody, chant it with me! “CORRELATION IS NOT CAUSATION!” Can we get it one more time for those at the back? “CORRELATION IS NOT CAUSATION!”

I take it most people have had this experience at morning-assembly in elementary school at one time or another… No? Just me? Well, most people have at least experienced something basically like this. It’s like the first thing you learn about statistics, before you even know what statistics is—it is bottle-fed to you by teachers, professors, and your smart-ass friends who want to look cool in an argument. Correlation is not causation—it’s the self-affirmation of fedora-wearing Free Thinkers, before they do their atheism-yoga and pray to Science in the morning.

There’s just one problem: It’s wrong.

---

---

Uhhh, well, I mean in this formulation it’s obviously true, actually: Correlation is not literally the same thing as causation, I’ll grant you that. Neither are they perfectly coextensive. The movement of my pinky in the next 10 seconds likely correlates with the movement of some other clump of matter somewhere in the universe, but they don’t cause each other.

However, the sentiment of the statement is incredibly wrong. Sure, correlation is not causation, but it’s evidence of causation. We may not always (or even usually) be justified in inferring from some correlation to a causal connection; still, the correlation will count in favor of there being a causal connection. Relying on the mantra “correlation is not causation” harms your brain more than TikTok screenmaxxing, as you end up classifying perfectly good inferences as “fallacious” when it’s convenient. One day you look yourself in the mirror and realize that you’re incapable of having a productive argument anymore, since no one can give you empirical evidence to convince you of some causal link you don’t already want to believe in.

If Hume is to be believed, the only way we learn about causation is through correlation—actually, causation just is correlation (WARNING: Oversimplification). This latter part may be disputable, but something along the lines of the former is clearly correct. I only know that forgetting to take my lunchbox out of my bag for days causes its insides to turn turquoise because I have seen that series of events play out many times (oops). Similarly, I only know that pressing this big beautiful blue button will cause you immeasurable pleasure because someone doing this is always followed by a book-length testimonial where the lucky person offers me their life-savings as thanks, and requests that I raise their children:

---

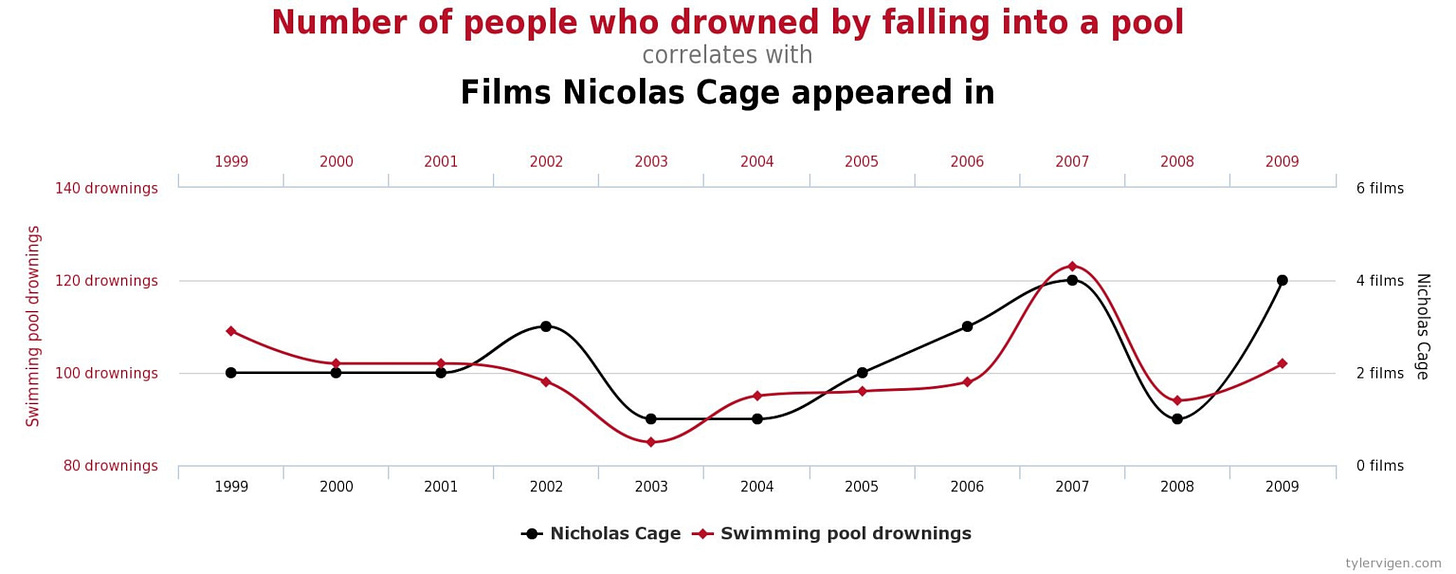
But surely I can’t seriously say that correlation is evidence of causation. I mean, we’ve probably all seen the following graph:

Omg, that’s so funny! This is, like, Proof that causation and correlation are not the same thing! No one would take this to show that Nicholas Cage causes people to drown.

That’s right, no one would and no one should. This doesn’t show that correlation isn’t evidence of causation, though. Rather it just points us in the direction of the more nuanced (and correct) view: Correlation is evidence of causation, but not conclusive evidence of causation (I know, I can already hear the brains exploding). Watch out, here comes the Bayesianism-stuff.

---

To show this, we don’t need some completely worked out metaphysical account of causation here. Rather we’ll just define it in a metaphysics-neutral way as: A (positively) causes B iff P(B|do(A))>P(B|do(¬A)).¹ (And P(B|do(A))=1 for deterministic causation.)

The “do(A)” operator here means that A is intervened to be the case, and we’re not just observing it to be the case. That is, we’re abstracting away the usual reasons why we might observe A. So it’s the difference between looking at some guy who owns a Labubu and checking whether he pretends to like iced vanilla matcha lattes,² vs. taking a guy, giving him a Labubu, and seeing whether that makes him drink matcha.

Also, we’ll define evidence as positive relevance: E is evidence for H iff P(H|E)>P(H). A useful equivalent of this is P(E|H)>P(E|¬H).

From here it should be obvious how it goes. Let’s say that H is the hypothesis that A positively causes B, and O be the observation that there’s some positive correlation between A and B. Now (barring a few qualifications we’ll get to), H will clearly predict O better than ¬H—meaning O will be evidence for H. After all, ¬H will include hypotheses that predict that we’d see no correlation, or even negative correlation. Updating on O, we disconfirm such hypotheses and so confirm H.

Or, well, not quite as straightforwardly. Other hypotheses will predict O equally well, or better. These might include there being a confounder, there being some selection effect, an evil demon beaming these sensory impressions into your mind, etc. Depending on your priors across these sorts of hypotheses, observing this correlation might actually be evidence against a causal link, oddly enough.

For example, suppose you observe some moderate correlation between reading Wonder and Aporia and being a cool person. Now, antecedently your entire credence-space is equally split between H1 that reading Wonder and Aporia causes you to be a cool person, and H2 that the confounder of liking philosophy causes both (this is realistic, I swear). Suppose further that while H1 predicts this moderate sort of correlation pretty well, H2 predicts it even better! In this case observing the correlation is actually evidence against H1.

However, if we add the hypothesis H3 that there’s no relation, then (depending on exactly how we set the numbers), observing the correlation can be evidence for both H1 and H2, while just being evidence against H3.

Also, there are some fun considerations regarding necessity, which I’ll put in this footnote for the readers who don’t slack off.³

---

Return to the Nicholas Cage example. Suppose this trend continued and continued. Every time Nicholas Cage starred in a movie there was a clear spike in deaths by drowning, and this kept being the case for decades. At that point you should begin to suspect that there really was some causal link—maybe people hate his movies so much that mere knowledge of another one existing out there fills them with despair, leaving suicide by drowning as the only option left (or something else, idk).

However, there’s nothing special about any of these individual cases of correlation. For each one, had you observed it in isolation, you wouldn’t conclude that there were some causal link. Rather each is some evidence, and as it cumulates, the null-hypothesis or other no-causal-connection hypotheses are disconfirmed more and more.

So why shouldn’t we just go around inferring causal links wherever we see any significant correlation? Well, because most things just don’t cause most things. Your prior that Nicholas Cage movies cause people to kill themselves (or drown otherwise) should be incredibly low (depending on how bad you think his movies are). So even though we see a clear correlation between the two over some time period, that doesn’t boost the cause-hypothesis enough.

And on top of that there are always competing hypotheses (e.g. confounders, coincidence, or the causation going the other way) which might have higher priors, or better predict the correlation. All of this is consistent with observing correlations being the only way you’re ever justified in inferring causation (barring indirect justifications like testimony).

To be fair to the original claim, there is a decent point buried somewhere in there. People are generally too prone to infer causal links where there are none. As such, the idea that correlation is not causation can be a pretty good heuristic, since correlations are usually not sufficient evidence to infer causation.

The problem is when you internalize this lesson a little too well—you take the heuristic at face value, and never trust an inference from correlation to causation. Or, not quite. Obviously you still do trust such inferences, as you’ll have beliefs about what causes what. It’s just that when pressed, you’ll deny any correlation that could show some causal link, if convenient. And importantly, you don’t need to provide any better alternative explanation or anything, you can just say “correlation≠causation” and be done with it. Free thinking accomplished.

You Might Also Like:

1. Switch the inequality for negative causation. I hope you can see how to modify what follows in this case.

2. Tbh, they do kinda taste pretty good.

3. Firstly, for a priori necessities (think logical truths, conceptual truths, etc.), under this way of conceptualizing causation we get the result that we could never discover any causes for these through correlation. After all, their probability should always be 1, regardless of whatever we plug in for do(X) (assuming logical omniscience and all that stuff)—hence the hypothesis that A causes B, where B is necessary, doesn’t make any predictions. Now, this also clearly seems to be the right verdict, as these necessities are not the sorts of things to be caused.

The interesting thing is when we consider things that are not actually necessary, but only epistemically necessary. Take the proposition “I exist” or something close enough, which is epistemically necessary—you could not find yourself in a position where you doubt it. Again, it seems that you could not discover any correlation to be evidence for any cause of this proposition. After all, whatever you observe, it will always correlate with this proposition being true.

This, however, is a little strange on the face of it. If the way we generally discover causal links is through observing correlations, this would seem to suggest that I could not discover the cause of my existence—at least not in anything resembling the normal way I discover causal links.

Nevertheless I think this is the right verdict. Imagine that you come into existence in a room with nothing resembling you around. How would you find out what caused your existence? Well, you couldn’t! You can’t make any observation that would be evidence that X caused your existence, since whether or not occurs X cannot in any way be discovered by you to have any connection to whether or not you exist—as you will always exist when you observe something.

How, then, do I find out the cause of my existence? After all, I really do know what caused my existence—my parents having sex (something I try not to think about too much). Well, you don’t actually infer the cause of your existence directly. Rather you assume that other things that appear to be like you (i.e. humans around you) are similar to you, and are also existing people. You can then observe that these things come into existence through people having sex and all that, and then infer that the same is probably the case for you.

So you really don’t infer the cause of your existence directly. In fact, you couldn’t do so, as your existence is not the sort of thing you can observe correlate differentially with different things. Instead you have to infer it through some assumptions regarding things that look like you.